树型结构

树型结构的基本概念

对大量的输入数据，链表的线性访问时间太慢，不宜使用。本文探讨另外一种重要的数据结构----树，其大部分时间可以保证操作的运行平均时间复杂度为O(logN)，第一部分先来看一下树的一些预备知识。

首先看一下树形结构的样子，下图代表的是树型结构的一般形态：

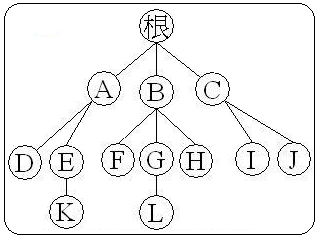
由上图看得出树是一些节点的集合，总结一下树的一些基本概念：

1. 结点：树中的数据元素都称之为结点
2. 根：最上面的结点称之为根，一颗树只有一个根且由根发展而来，从另外一个角度来说，每个结点都可以认为是其子树的根
3. 父亲：结点的上层结点，如图中，结点K的父亲是E、结点L的父亲是G
4. 兄弟：具有相同父亲的结点称为兄弟，图中F、G、H互为兄弟
5. 结点的度：结点所拥有的子树的个数称之为结点的度，如结点B的度为3
6. 树叶：度为0的结点，也叫作终端结点，图中D、K、F、L、H、I、J都是树叶
7. 分支结点：度不为0的结点，也叫作非终端结点或内部结点，图中根、A、B、C、E、G都是分支结点
8. 结点的层次：从根节点到树中某结点所经路径上的分支树称为该结点的层次，根节点的层次规定为1，其余结点的层次等于其父亲结点的层次+1
9. 树的深度：树中结点的最大层次数，图中树的深度为4

二叉树

上面的是树的一般形态，下面看一下二叉树。二叉树是一棵树，其中每个结点都不能有多于两个子树。

下图展示了一颗二叉树：

二叉树的一个性质是一颗平均二叉树的深度要比及结点个数N小得多，这个性质很重要，尤其对于特殊类型的二叉树即二叉查找树而言，其深度的平均值是O(logN)，这将大大降低查找时的时间复杂度。

当然，二叉树在运用得不好的情况下的情况下是有严重的问题的，即：

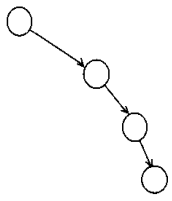
树的深度大到了N-1，这样的情况是绝对不允许的，这种树也被称为不平衡树。在下一部分的二叉查找树说明完之后，会讲让二叉树带有自平衡条件，成为平衡树。

二叉查找树

二叉树的一个重要应用是在它们查找中的使用。假设树中的每个结点存储一项数据，使得二叉树成为二叉查找树的性质是：对于树中的每个结点X，它的左子树中所有项的值小于X，而它的右子树中所有项的值大于X，这意味着该树所有的元素可以用某种一致的方式排序。

如下图：

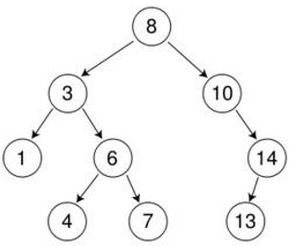
这就是一个二叉查找树。但是如果我这么修改一下：

这就不是一个二叉查找树了，因为在根节点的左子树中，有一个节点是11。

AVL树

前面已经讲到过了，在生成二叉树/二叉查找树的时候是非常容易失衡的，造成的最坏的情况就是一边倒（只有左子树/右子树），这样将会导致树的检索效率大大降低，所以为了维持二叉树的平衡，大牛们提出了各种实现的算法，如：AVL树、节点大小平衡树（SBT）、伸展树、树堆（Treap）、红黑树等等。

这里讲AVL树----一种带有平衡条件的二叉查找树，这种平衡条件必须要容易保持，而且它保证树的深度必须是O(logN)。

对于AVL树来说，它的平衡必须满足以下特征之一：

1. 空树
2. 每个结点的左子树和右子树深度最多差1

可以看一下下图：

图中，左边的树是AVL树，右边的树不是。因为很显然，从根结点7看起，右子树的深度为1，而左子树7-->2-->4-->5(3)这条路径深度为3，不满足每个结点的左子树和右子树深度最多差1的条件。

可以证明，一颗AVL树的高度最多为1.44 * log(N + 2) - 1.328，但是实际上的高度只略大于logN。

红黑树

红黑树是对AVL树的另一种变种。红黑树顾名思义就是结点是红色或者黑色的平衡二叉树，它通过颜色的约束来维持着二叉树的平衡。下图为一颗典型的二叉树：

对于一颗有效的红黑树而言我们必须增加如下规则：

1. 每个结点都只能是红色或者黑色
2. 根节点是黑色
3. 每片叶子都是黑色的
4. 如果一个结点是红色的，则它的两个子节点都是黑色的，也就是说在一条路径上不能出现相邻的两个红色结点
5. 从任意一个结点到其每个叶子的所有路径都包含着相同数目的黑色结点

这些约束强制了红黑树的关键性质：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果就是这棵树大致上是平衡的，因为插入、删除和查找某个值得最坏情况时间都要求与树的高度成比例，这个高度理论上限允许红黑树只在最坏情况下都是高效的。

再具体就不说了，可以参看http://www.cnblogs.com/yangecnu/p/Introduce-Red-Black-Tree.html，对红黑树的讲解写得非常好。

对了，TreeMap和TreeSet就是红黑树的典型实现。

来源：https://www.cnblogs.com/xrq730/p/5187032.html